En navegación, la actitud se refiere a la orientación de un vehículo u objeto con respecto a un marco de referencia fijo, que suele definirse mediante tres ejes de rotación: cabeceo (pitch), balanceo (roll) y guiñada (raw).
Estos ejes describen la posición angular y el movimiento del vehículo en el espacio tridimensional. cabeceo (pitch) se refiere a la inclinación hacia arriba o hacia abajo del morro del vehículo, balanceo (roll) representa la inclinación lateral del vehículo a lo largo de su eje longitudinal, y guiñada (raw) denota la rotación a izquierda o derecha alrededor de su eje vertical. Juntos, estos parámetros definen cómo se posiciona y maniobra un vehículo en su entorno.
La actitud es crucial para mantener la estabilidad, garantizar un control preciso y permitir una navegación exacta en diversos ámbitos. En la aviación, por ejemplo, la actitud ayuda a los pilotos o a los sistemas de piloto automático a mantener un vuelo nivelado, ejecutar giros y ajustarse a las turbulencias.
Del mismo modo, en la navegación marítima, el control de la actitud garantiza que un buque se mantenga en posición vertical y en curso a pesar de los desafíos que plantean las olas y las corrientes.
En las naves espaciales, la actitud desempeña un papel fundamental a la hora de orientar antenas, paneles solares o instrumentos científicos en la dirección correcta, especialmente cuando no se dispone de señales visuales externas.
Para medir y controlar la actitud, se emplean sistemas como giroscopios, acelerómetros y magnetómetros, a menudo integrados en un sistema de navegación inercial (INS). Estos sistemas funcionan en conjunción con fuentes de datos externas, como GNSS o rastreadores de estrellas, para mantener una orientación precisa.
Comprender y gestionar la actitud es especialmente importante en entornos dinámicos, donde fuerzas externas como el viento, las olas o las anomalías gravitatorias pueden afectar a la trayectoria de un vehículo.
Un control eficaz de la actitud, por tanto, garantiza un desplazamiento seguro y eficiente, permitiendo a los vehículos cumplir sus objetivos de navegación con precisión.
Soluciones de actitud GNSS
Las soluciones de actitud GNSS proporcionan los ángulos de balanceo (roll), cabeceo (pitch) y guiñada (raw) , que describen la orientación de un objeto en el espacio. Estos tres componentes son esenciales para comprender la actitud del objeto respecto a la superficie terrestre o a un marco de referencia.
- balanceo (roll) se refiere a la rotación alrededor del eje delantero, que afecta a la inclinación izquierda y derecha del objeto.
- cabeceo (pitch) es la rotación alrededor del eje lateral, que determina la inclinación hacia arriba y hacia abajo.
- guiñada (raw) es la rotación alrededor del eje vertical, que define la dirección en la que está orientado el objeto.
Estas soluciones combinan datos de receptores GNSS con sensores adicionales, como acelerómetros y giroscopios, para proporcionar información de actitud muy precisa y fiable.
Este enfoque es especialmente valioso en entornos en los que la orientación precisa es crucial, como en los sistemas de navegación de aviones, barcos y vehículos autónomos. Gracias a la integración de estos diversos sensores, el sistema garantiza un rendimiento óptimo incluso en condiciones difíciles.
Representaciones de actitudes
La actitud representa la orientación o rotación de un objeto con respecto a un marco de referencia, como la superficie terrestre. En los sistemas de navegación, este concepto es fundamental para determinar la orientación del objeto en el espacio, lo que podría aplicarse a aeronaves, vehículos aéreos no tripulados, barcos u otros sistemas autónomos. Hay varias formas de representar la actitud matemática y visualmente.
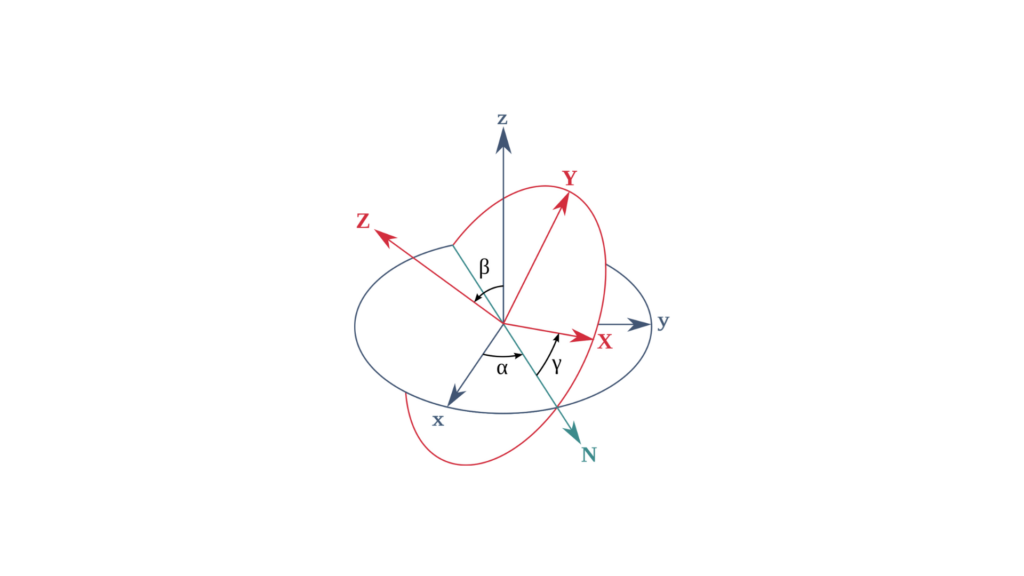
1 - Ángulos de Eulerbalanceo (roll), cabeceo (pitch), guiñada (raw))
Los ángulos de Euler representan la orientación de un objeto mediante tres rotaciones: balanceo (roll), cabeceo (pitch) y guiñada (raw). Estos ángulos describen rotaciones alrededor de tres ejes en una secuencia específica, como:
balanceo (roll) (φ): Rotación alrededor del eje antero-posterior.
cabeceo (pitch) (θ): Rotación alrededor del eje de lado a lado.
guiñada (raw) (ψ): Rotación alrededor del eje vertical.
Representación matemática
Los ángulos de Euler pueden representarse como una matriz de rotación 3×3, donde:
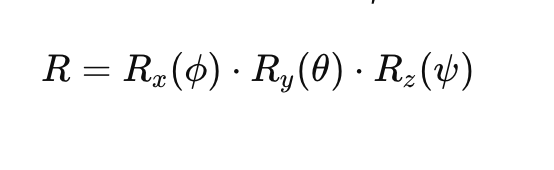
Toma:
- Rx(ϕ)R_x(\phi)Rx(ϕ) es la matriz de rotación balanceo (roll).
- Ry(θ)R_y(\theta)Ry(θ) es la matriz de rotación para cabeceo (pitch).
- Rz(ψ)R_z(\psi)Rz(ψ) es la matriz de rotación de guiñada (raw).
Cada matriz de rotación viene dada como:
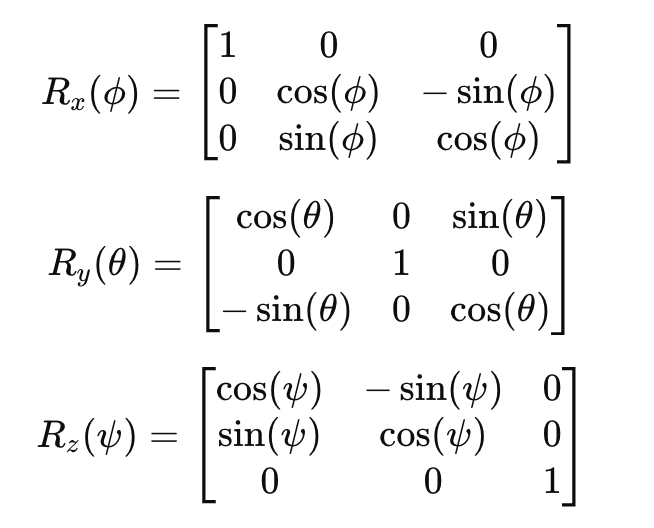
2 - Matrices de rotación
Las matrices de rotación ofrecen una forma alternativa de representar la actitud. En este método, una matriz de 3×3 describe la orientación de un objeto en el espacio tridimensional con respecto a un sistema de coordenadas fijo. Estas matrices son ortogonales, lo que significa que las filas y las columnas son vectores unitarios. Por consiguiente, la inversa de la matriz es simplemente su transpuesto.
Representación matemática
Se puede escribir una matriz de rotación general 𝑅 como:
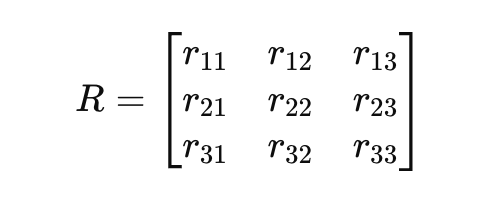
3 - Cuaterniones
Los cuaterniones ofrecen una representación de la rotación más compacta y numéricamente estable. Evitan las singularidades y los problemas de bloqueo del cardán asociados a los ángulos de Euler. Un cuaternión 𝑞 es un vector de 4 dimensiones:
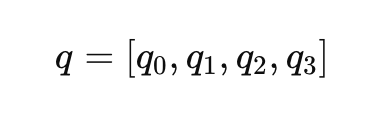
Donde 𝑞0 es la parte escalar, y [𝑞1, 𝑞2, 𝑞3] son las componentes vectoriales. La representación en cuaterniones de una rotación puede escribirse como:
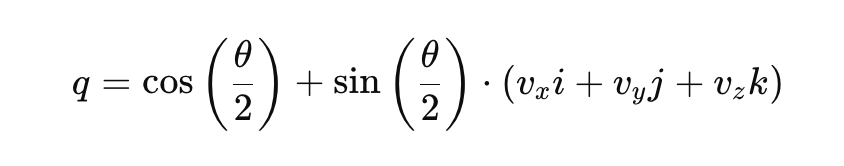
Toma:
- θ es el ángulo de rotación.
- [vx,vy,vz] es el vector unitario que representa el eje de rotación.
- i, j, k son las unidades fundamentales del cuaternión.
Ventajas de los cuaterniones:
- Evita el bloqueo del cardán y las singularidades.
- Más eficiente computacionalmente para la interpolación.
4 - Matrices coseno-direccionales (MCD)
Una matriz de coseno de dirección es similar a una matriz de rotación y también describe la orientación de un objeto. La MCD relaciona las coordenadas de un vector en un fotograma con las coordenadas del mismo vector en otro fotograma.
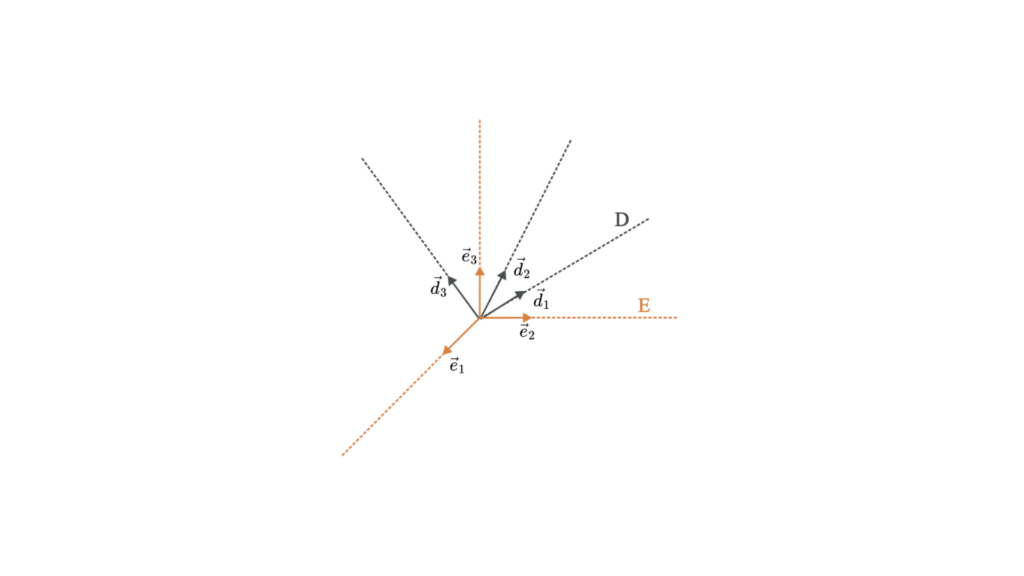
Representación matemática
Una matriz de coseno de dirección 𝐶 es una matriz de 3×3 que define la relación entre dos marcos de coordenadas:
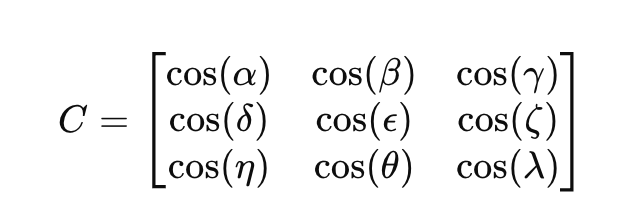
Donde los elementos cos (⋅) representan el coseno del ángulo entre los vectores de los dos marcos de coordenadas.
Háblenos de su proyecto