En navigation, l'attitude fait référence à l'orientation d'un véhicule ou d'un objet par rapport à un repère fixe, qui est généralement défini par trois axes de rotation : le tangage, le roulis et le lacet.
Ces axes décrivent la position angulaire et le mouvement du véhicule dans l'espace tridimensionnel. Le tangage fait référence à l'inclinaison vers le haut ou vers le bas du nez du véhicule, le roulis représente l'inclinaison latérale du véhicule le long de son axe longitudinal, et le lacet indique la rotation vers la gauche ou vers la droite autour de son axe vertical. Ensemble, ces paramètres définissent la manière dont un véhicule est positionné et manœuvré dans son environnement.
L'attitude est essentielle pour maintenir la stabilité, assurer un contrôle précis et permettre une navigation précise dans divers domaines. Dans l'aviation, par exemple, l'attitude aide les pilotes ou les systèmes de pilotage automatique à maintenir un vol en palier, à exécuter des virages et à s'adapter aux turbulences.
De même, dans la navigation maritime, le contrôle de l'attitude garantit qu'un navire reste droit et sur sa trajectoire malgré les défis posés par les vagues et les courants.
Dans les engins spatiaux, l'attitude joue un rôle essentiel dans le pointage des antennes, des panneaux solaires ou des instruments scientifiques dans la bonne direction, en particulier lorsque les repères visuels externes ne sont pas disponibles.
Pour mesurer et contrôler l'attitude, des systèmes tels que les gyroscopes, les accéléromètres et les magnétomètres sont utilisés, souvent intégrés dans un système de navigation inertielle (INS). Ces systèmes fonctionnent en conjonction avec des sources de données externes telles que le GNSS ou les suiveurs d'étoiles pour maintenir une orientation précise.
La compréhension et la gestion de l'attitude sont particulièrement importantes dans les environnements dynamiques, où les forces externes telles que le vent, les vagues ou les anomalies gravitationnelles peuvent avoir un impact sur la trajectoire d'un véhicule.
Un contrôle efficace de l'attitude garantit donc un déplacement sûr et efficace, permettant aux véhicules d'atteindre leurs objectifs de navigation avec précision.
Solutions d'attitude GNSS
Les solutions d'attitude GNSS fournissent les angles de roulis, de tangage et de lacet, qui décrivent l'orientation d'un objet dans l'espace. Ces trois composantes sont essentielles pour comprendre l'attitude de l'objet par rapport à la surface de la Terre ou à un référentiel.
- Le roulis fait référence à la rotation autour de l'axe avant, affectant l'inclinaison gauche et droite de l'objet.
- Le tangage est la rotation autour de l'axe latéral, déterminant l'inclinaison de haut en bas.
- Le lacet est la rotation autour de l'axe vertical, qui définit la direction vers laquelle l'objet est orienté.
Ces solutions combinent les données des récepteurs GNSS avec des capteurs supplémentaires, tels que des accéléromètres et des gyroscopes, pour fournir des informations très précises et fiables sur l'attitude.
Cette approche est particulièrement utile dans les environnements où une orientation précise est cruciale, comme dans les systèmes de navigation pour les avions, les navires et les véhicules autonomes. En intégrant ces différents capteurs, le système garantit des performances optimales, même dans des conditions difficiles.
Représentations de l'attitude
L'attitude représente l'orientation ou la rotation d'un objet par rapport à un référentiel, tel que la surface de la Terre. Dans les systèmes de navigation, ce concept est essentiel pour déterminer l'orientation de l'objet dans l'espace, ce qui peut s'appliquer aux aéronefs, aux UAV, aux navires ou à d'autres systèmes autonomes. Il existe plusieurs façons de représenter l'attitude mathématiquement et visuellement.
1 – Angles d'Euler (Roulis, Tangage, Lacet)
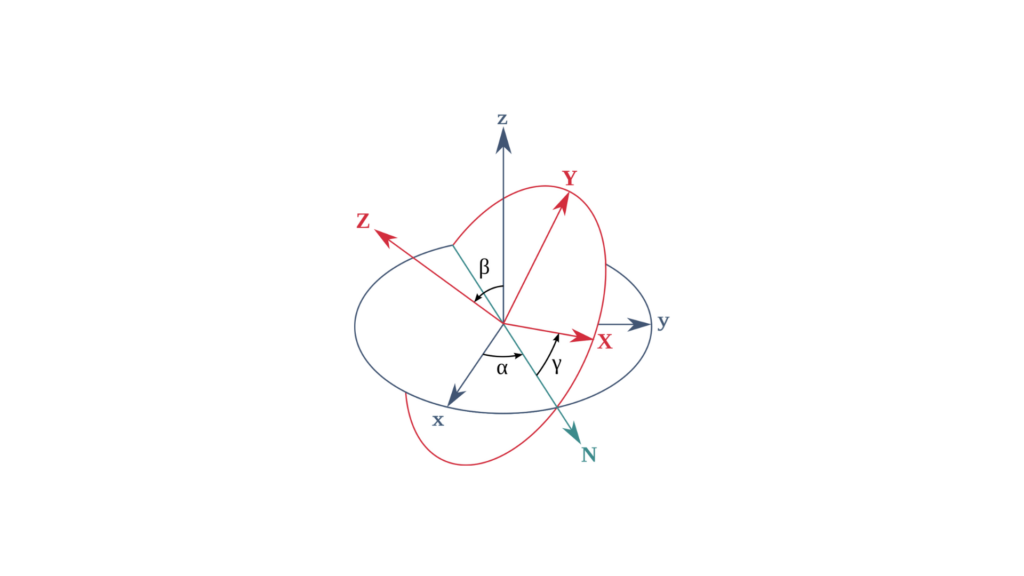
Les angles d'Euler représentent l'orientation d'un objet par trois rotations : roulis, tangage et lacet. Ces angles décrivent les rotations autour de trois axes dans une séquence spécifique, telle que :
Roulis (φ) : Rotation autour de l'axe avant-arrière.
Tangage (θ) : Rotation autour de l'axe latéral.
Lacet (ψ) : Rotation autour de l'axe vertical.
Représentation mathématique
Les angles d'Euler peuvent être représentés par une matrice de rotation 3×3, où :
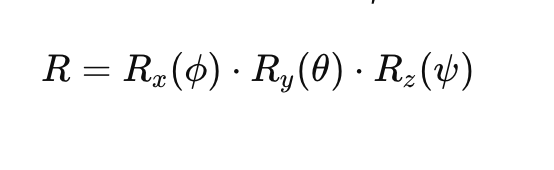
Ici :
- Rx(ϕ)R_x(\phi)Rx(ϕ) est la matrice de rotation pour le roulis.
- Ry(θ)R_y(\theta)Ry(θ) est la matrice de rotation pour le tangage.
- Rz(ψ)R_z(\psi)Rz(ψ) est la matrice de rotation pour le lacet.
Chaque matrice de rotation est donnée comme :
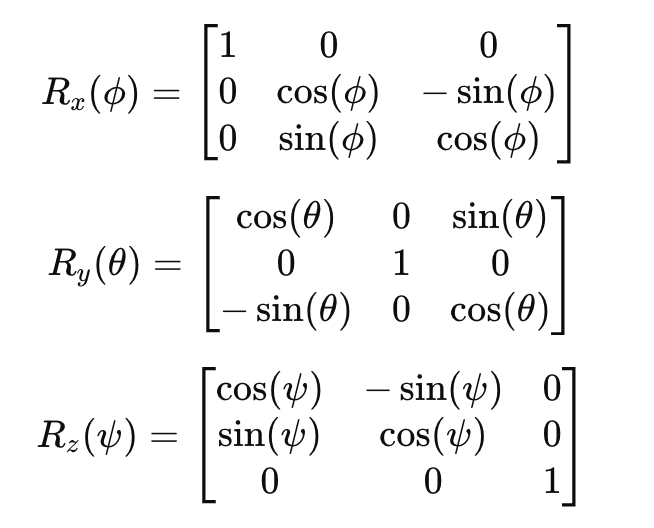
2 – Matrices de rotation
Les matrices de rotation offrent une autre façon de représenter l'attitude. Dans cette méthode, une matrice 3×3 décrit l'orientation d'un objet dans l'espace 3D par rapport à un système de coordonnées fixe. Ces matrices sont orthogonales, ce qui signifie que les rangées et les colonnes sont des vecteurs unitaires. Par conséquent, l'inverse de la matrice est simplement sa transposée.
Représentation mathématique
Vous pouvez écrire une matrice de rotation générale 𝑅 comme suit :
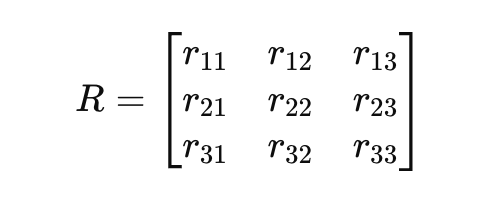
3 – Quaternions
Les quaternions fournissent une représentation plus compacte et numériquement stable de la rotation. Ils évitent les singularités et les problèmes de blocage de cardan associés aux angles d'Euler. Un quaternion 𝑞 est un vecteur à 4 dimensions :
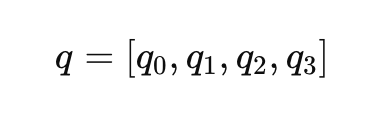
Où 𝑞0 est la partie scalaire et [𝑞1, 𝑞2, 𝑞3] sont les composantes vectorielles. La représentation en quaternions d'une rotation peut s'écrire comme suit :
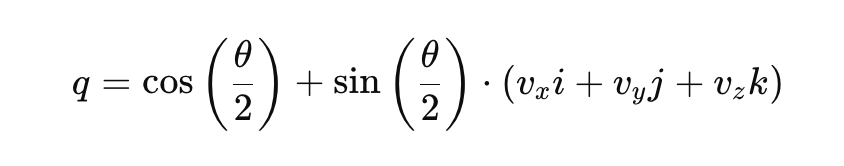
Ici :
- θ est l'angle de rotation.
- [vx,vy,vz] est le vecteur unitaire représentant l'axe de rotation.
- i, j, k sont les unités fondamentales des quaternions.
Avantages des Quaternions :
- Évite le blocage de cardan et les singularités.
- Plus efficace en termes de calcul pour l'interpolation.
4 – Matrices de cosinus directeurs (DCM)
Une matrice de cosinus directeurs est similaire à une matrice de rotation et décrit également l'orientation d'un objet. La DCM relie les coordonnées d'un vecteur dans un repère aux coordonnées du même vecteur dans un autre repère.
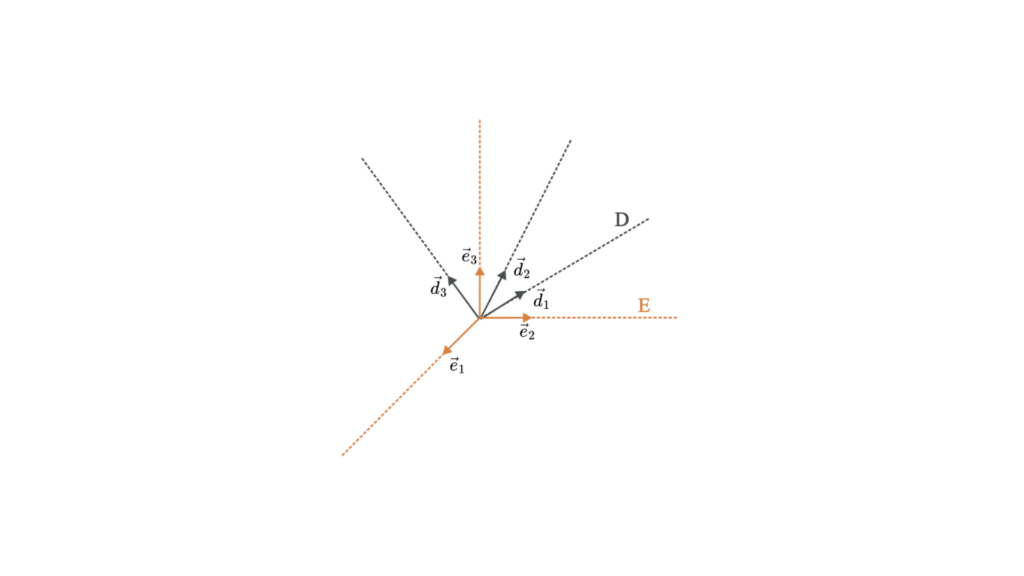
Représentation mathématique
Une matrice de cosinus directeurs 𝐶 est une matrice 3 × 3 qui définit la relation entre deux repères :
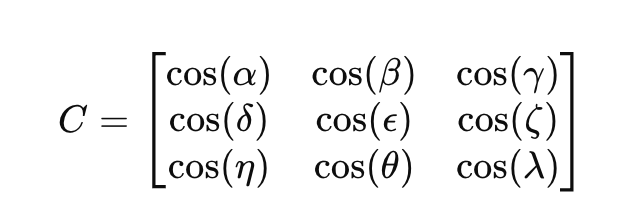
Où les éléments cos (⋅) représentent le cosinus de l'angle entre les vecteurs des deux cadres de coordonnées.
Parlez-nous de votre projet