Em navegação, atitude se refere à orientação de um veículo ou objeto em relação a um sistema de referência fixo, que normalmente é definido por três eixos rotacionais: arfagem (pitch), rolamento (roll) e guinada (yaw).
Esses eixos descrevem a posição angular e o movimento do veículo no espaço tridimensional. Arfagem (pitch) se refere à inclinação para cima ou para baixo da frente do veículo, rolamento (roll) representa a inclinação lateral do veículo ao longo de seu eixo longitudinal e guinada (yaw) denota a rotação para a esquerda ou para a direita em torno de seu eixo vertical. Juntos, esses parâmetros definem como um veículo é posicionado e manobrado em seu ambiente.
A atitude é crucial para manter a estabilidade, garantir o controle preciso e permitir a navegação precisa em vários domínios. Na aviação, por exemplo, a atitude ajuda os pilotos ou sistemas de piloto automático a manter o voo nivelado, executar curvas e ajustar-se à turbulência.
Da mesma forma, na navegação marítima, o controle de atitude garante que uma embarcação permaneça na vertical e no curso, apesar dos desafios impostos pelas ondas e correntes.
Em espaçonaves, a atitude desempenha um papel crítico no apontamento de antenas, painéis solares ou instrumentos científicos na direção correta, especialmente quando as pistas visuais externas não estão disponíveis.
Para medir e controlar a atitude, sistemas como giroscópios, acelerômetros e magnetômetros são empregados, frequentemente integrados a um Sistema de Navegação Inercial (INS). Esses sistemas trabalham em conjunto com fontes de dados externas, como GNSS ou rastreadores de estrelas, para manter a orientação precisa.
Compreender e gerenciar a atitude é particularmente importante em ambientes dinâmicos, onde forças externas como vento, ondas ou anomalias gravitacionais podem impactar a trajetória de um veículo.
O controle de atitude eficaz, portanto, garante uma viagem segura e eficiente, permitindo que os veículos atinjam seus objetivos de navegação com precisão.
Soluções de atitude GNSS
As soluções de atitude GNSS fornecem os ângulos de roll, pitch e yaw, que descrevem a orientação de um objeto no espaço. Esses três componentes são essenciais para entender a atitude do objeto em relação à superfície da Terra ou a um sistema de referência.
- Rolagem refere-se à rotação em torno do eixo frontal, afetando a inclinação esquerda e direita do objeto.
- Arfagem é a rotação em torno do eixo transversal, que determina a inclinação vertical.
- Yaw é a rotação em torno do eixo vertical, que define a direção para a qual o objeto está voltado.
Essas soluções combinam dados de receptores GNSS com sensores adicionais, como acelerômetros e giroscópios, para fornecer informações de atitude altamente precisas e confiáveis.
Essa abordagem é particularmente valiosa em ambientes onde a orientação precisa é crucial, como em sistemas de navegação para aeronaves, embarcações e veículos autônomos. Ao integrar essas diversas entradas de sensores, o sistema garante um desempenho ideal, mesmo em condições desafiadoras.
Representações de Atitude
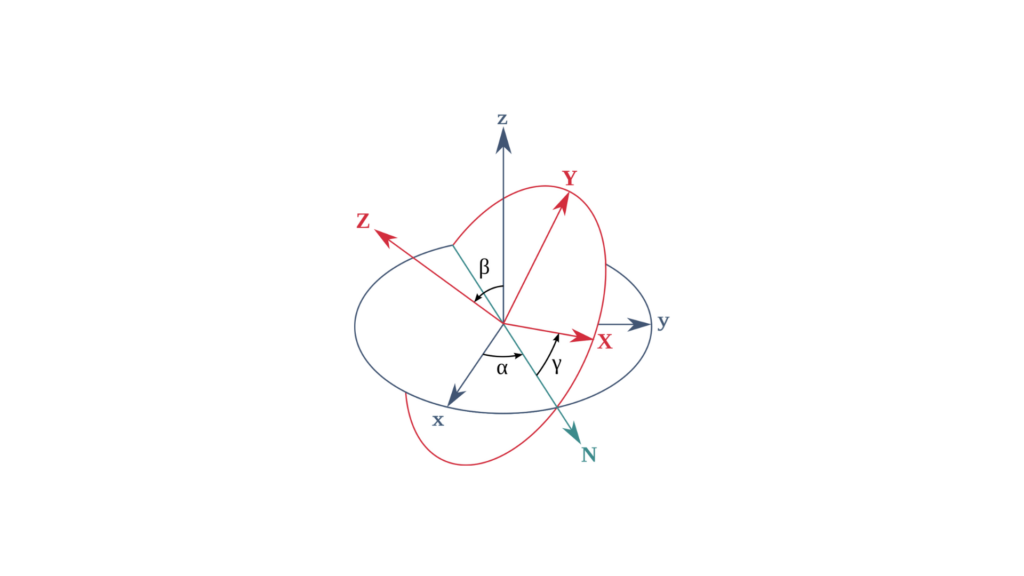
Atitude representa a orientação ou rotação de um objeto em relação a um referencial, como a superfície da Terra. Em sistemas de navegação, este conceito é crítico para determinar a orientação do objeto no espaço, o que pode ser aplicado a aeronaves, UAVs, navios ou outros sistemas autônomos. Existem várias formas de representar a atitude matematicamente e visualmente.
1 – Ângulos de Euler (Roll, Pitch, Yaw)
Os ângulos de Euler representam a orientação de um objeto através de três rotações: roll, pitch e yaw. Esses ângulos descrevem as rotações em torno de três eixos em uma sequência específica, como:
Roll (φ): Rotação em torno do eixo frontal-traseiro.
Pitch (θ): Rotação em torno do eixo lateral.
Yaw (ψ): Rotação em torno do eixo vertical.
Representação Matemática
Os ângulos de Euler podem ser representados como uma matriz de rotação 3×3, onde:
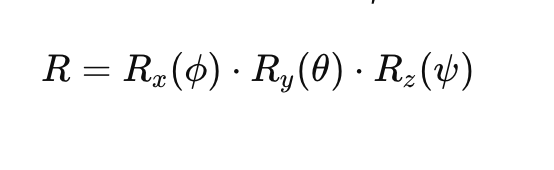
Aqui:
- Rx(ϕ)R_x(\phi)Rx(ϕ) é a matriz de rotação para rolamento.
- Ry(θ)R_y(\theta)Ry(θ) é a matriz de rotação para arfagem.
- Rz(ψ)R_z(\psi)Rz(ψ) é a matriz de rotação para guinada.
Cada matriz de rotação é dada como:
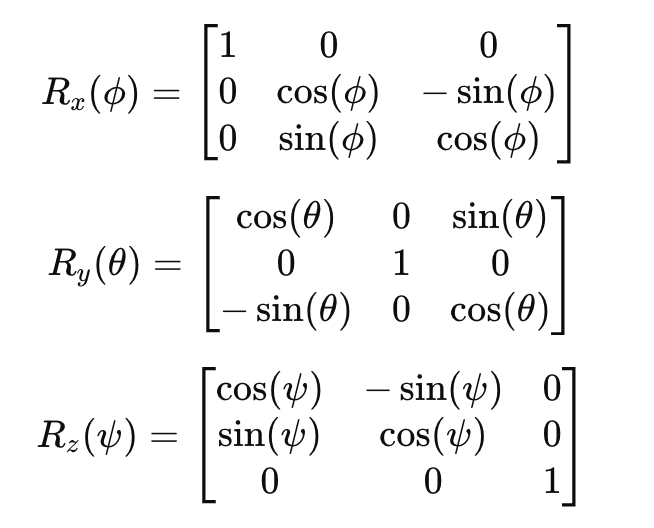
2 – Matrizes de Rotação
As matrizes de rotação oferecem uma forma alternativa de representar a atitude. Neste método, uma matriz 3×3 descreve a orientação de um objeto no espaço 3D em relação a um sistema de coordenadas fixo. Essas matrizes são ortogonais, o que significa que as linhas e colunas são vetores unitários. Consequentemente, a inversa da matriz é simplesmente sua transposta.
Representação Matemática
Você pode escrever uma matriz de rotação geral 𝑅 como:
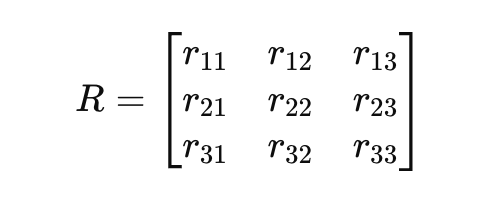
3 – Quaternions
Os quatérnios fornecem uma representação mais compacta e numericamente estável da rotação. Eles evitam singularidades e problemas de bloqueio de gimbal associados aos ângulos de Euler. Um quatérnio 𝑞 é um vetor de 4 dimensões:
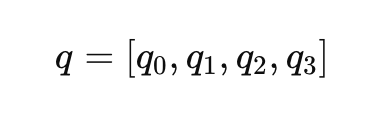
Onde 𝑞0 é a parte escalar, e [𝑞1, 𝑞2, 𝑞3] são os componentes vetoriais. A representação de quatérnio de uma rotação pode ser escrita como:
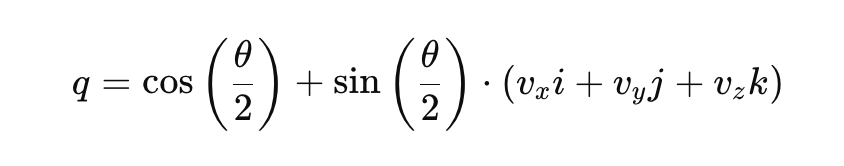
Aqui:
- θ é o ângulo de rotação.
- [vx,vy,vz] é o vetor unitário que representa o eixo de rotação.
- i, j, k são as unidades fundamentais do quatérnio.
Vantagens dos Quaternions:
- Evita o bloqueio do gimbal e singularidades.
- Mais eficiente computacionalmente para interpolação.
4 – Matrizes de Cosseno Diretor (DCM)
Uma matriz de cosseno de direção é semelhante a uma matriz de rotação e também descreve a orientação de um objeto. A DCM relaciona as coordenadas de um vetor em um sistema com as coordenadas do mesmo vetor em outro sistema.
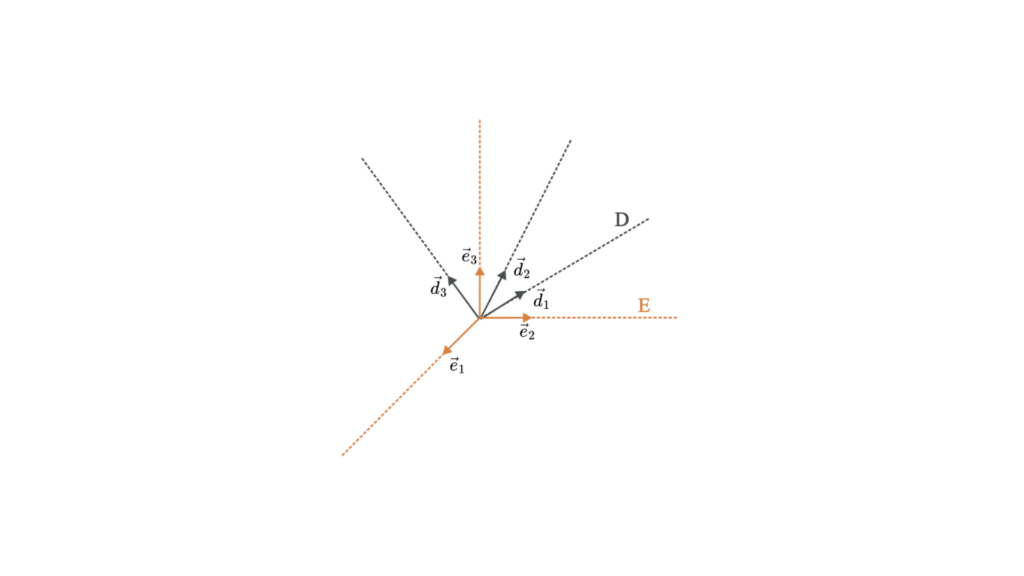
Representação Matemática
Uma matriz de cosseno de direção 𝐶 é uma matriz 3×3 que define a relação entre dois sistemas de coordenadas:
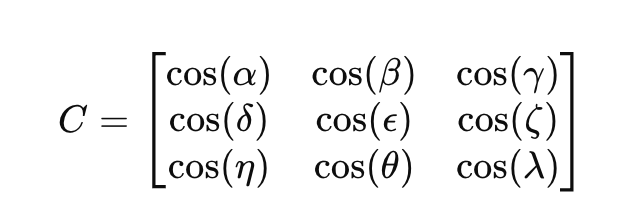
Onde os elementos cos (⋅) representam o cosseno do ângulo entre os vetores dos dois sistemas de coordenadas.
Fale-nos sobre seu projeto