Nella navigazione, l'assetto si riferisce all'orientamento di un veicolo o oggetto rispetto a un sistema di riferimento fisso, che è tipicamente definito da tre assi di rotazione: beccheggio, rollio e imbardata.
Questi assi descrivono la posizione angolare e il movimento del veicolo nello spazio tridimensionale. Il beccheggio si riferisce all'inclinazione verso l'alto o verso il basso del muso del veicolo, il rollio rappresenta l'inclinazione laterale del veicolo lungo il suo asse longitudinale e l'imbardata indica la rotazione a sinistra o a destra attorno al suo asse verticale. Insieme, questi parametri definiscono come un veicolo è posizionato e manovrato nel suo ambiente.
L'assetto è fondamentale per mantenere la stabilità, garantire un controllo preciso e consentire una navigazione accurata in vari domini. In aviazione, ad esempio, l'assetto aiuta i piloti o i sistemi di pilota automatico a mantenere il volo livellato, eseguire virate e adattarsi alle turbolenze.
Allo stesso modo, nella navigazione marittima, il controllo dell'assetto assicura che un'imbarcazione rimanga in posizione verticale e sulla rotta giusta nonostante le sfide poste da onde e correnti.
Nei veicoli spaziali, l'assetto svolge un ruolo fondamentale nel puntare antenne, pannelli solari o strumenti scientifici nella direzione corretta, soprattutto quando non sono disponibili segnali visivi esterni.
Per misurare e controllare l'assetto, vengono impiegati sistemi come giroscopi, accelerometri e magnetometri, spesso integrati in un Inertial Navigation System (INS). Questi sistemi lavorano in combinazione con fonti di dati esterne come il GNSS o gli star tracker per mantenere un orientamento accurato.
Comprendere e gestire l'assetto è particolarmente importante in ambienti dinamici, dove forze esterne come il vento, le onde o le anomalie gravitazionali possono influire sulla traiettoria di un veicolo.
Un efficace controllo dell'assetto, quindi, garantisce un viaggio sicuro ed efficiente, consentendo ai veicoli di raggiungere i loro obiettivi di navigazione con precisione.
Soluzioni di assetto GNSS
Le soluzioni di assetto GNSS forniscono gli angoli di rollio, beccheggio e imbardata, che descrivono l'orientamento di un oggetto nello spazio. Queste tre componenti sono essenziali per comprendere l'assetto dell'oggetto rispetto alla superficie terrestre o a un sistema di riferimento.
- Il rollio si riferisce alla rotazione attorno all'asse longitudinale, che influisce sull'inclinazione a sinistra e a destra dell'oggetto.
- Il beccheggio è la rotazione attorno all'asse laterale, che determina l'inclinazione verso l'alto e verso il basso.
- Lo Yaw è la rotazione attorno all'asse verticale, che definisce la direzione verso cui è rivolto l'oggetto.
Queste soluzioni combinano i dati dei ricevitori GNSS con sensori aggiuntivi, come accelerometri e giroscopi, per fornire informazioni sull'assetto estremamente accurate e affidabili.
Questo approccio è particolarmente valido in ambienti in cui un orientamento preciso è fondamentale, come nei sistemi di navigazione per aeromobili, navi e veicoli autonomi. Integrando questi diversi input dei sensori, il sistema garantisce prestazioni ottimali anche in condizioni difficili.
Rappresentazioni dell'assetto
L'assetto rappresenta l'orientamento o la rotazione di un oggetto rispetto a un sistema di riferimento, come la superficie terrestre. Nei sistemi di navigazione, questo concetto è fondamentale per determinare l'orientamento dell'oggetto nello spazio, il che potrebbe valere per aeromobili, UAV, navi o altri sistemi autonomi. Esistono diversi modi per rappresentare l'assetto matematicamente e visivamente.
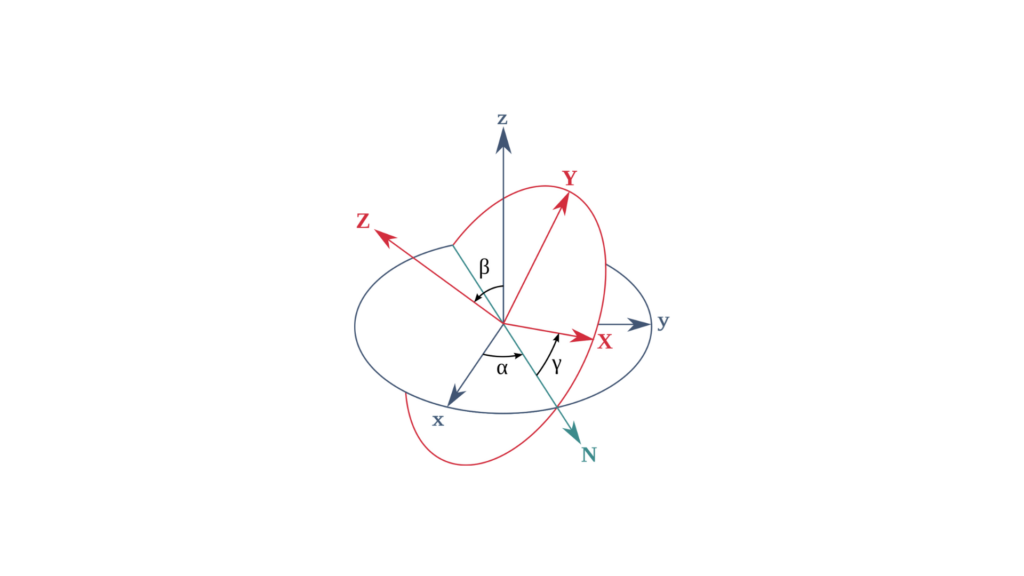
1 – Angoli di Eulero (Rollio, Beccheggio, Imbardata)
Gli angoli di Eulero rappresentano l'orientamento di un oggetto attraverso tre rotazioni: rollio, beccheggio e imbardata. Questi angoli descrivono le rotazioni attorno a tre assi in una sequenza specifica, come:
Roll (φ): Rotazione attorno all'asse anteriore-posteriore.
Pitch (θ): Rotazione attorno all'asse laterale.
Yaw (ψ): Rotazione attorno all'asse verticale.
Rappresentazione matematica
Gli angoli di Eulero possono essere rappresentati come una matrice di rotazione 3×3, dove:
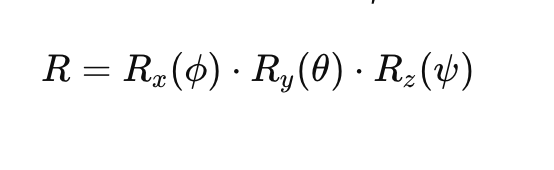
Qui:
- Rx(ϕ)R_x(\phi)Rx(ϕ) è la matrice di rotazione per il rollio.
- Ry(θ)R_y(\theta)Ry(θ) è la matrice di rotazione per il beccheggio.
- Rz(ψ)R_z(\psi)Rz(ψ) è la matrice di rotazione per l'imbardata.
Ogni matrice di rotazione è data come:
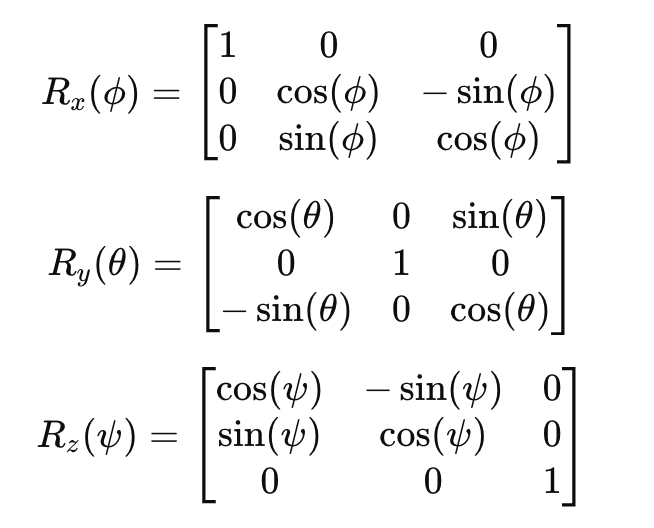
2 – Matrici di rotazione
Le matrici di rotazione offrono un modo alternativo per rappresentare l'assetto. In questo metodo, una matrice 3×3 descrive l'orientamento di un oggetto nello spazio 3D rispetto a un sistema di coordinate fisso. Queste matrici sono ortogonali, il che significa che le righe e le colonne sono vettori unitari. Di conseguenza, l'inversa della matrice è semplicemente la sua trasposta.
Rappresentazione matematica
È possibile scrivere una matrice di rotazione generale 𝑅 come:
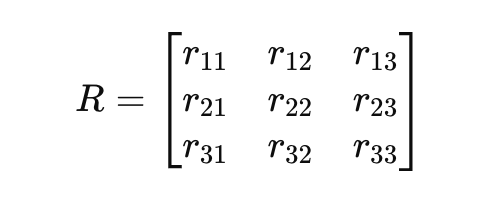
3 – Quaternioni
I quaternioni forniscono una rappresentazione più compatta e numericamente stabile della rotazione. Evitano singolarità e problemi di gimbal lock associati agli angoli di Eulero. Un quaternione 𝑞 è un vettore a 4 dimensioni:
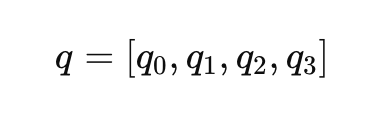
Dove 𝑞0 è la parte scalare e [𝑞1, 𝑞2, 𝑞3] sono le componenti vettoriali. La rappresentazione quaternionica di una rotazione può essere scritta come:
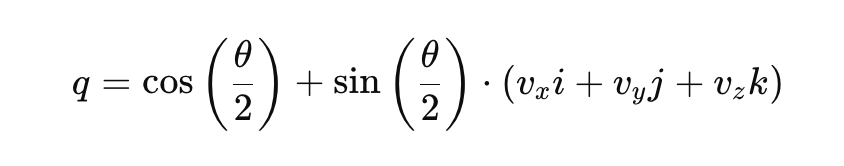
Qui:
- θ è l'angolo di rotazione.
- [vx,vy,vz] è il vettore unitario che rappresenta l'asse di rotazione.
- i, j, k sono le unità quaternion fondamentali.
Vantaggi dei Quaternioni:
- Evita il blocco cardanico e le singolarità.
- Maggiore efficienza computazionale per l'interpolazione.
4 – Matrici dei coseni direttori (DCM)
Una matrice di coseni direttori è simile a una matrice di rotazione e descrive anche l'orientamento di un oggetto. La DCM mette in relazione le coordinate di un vettore in un sistema con le coordinate dello stesso vettore in un altro sistema.
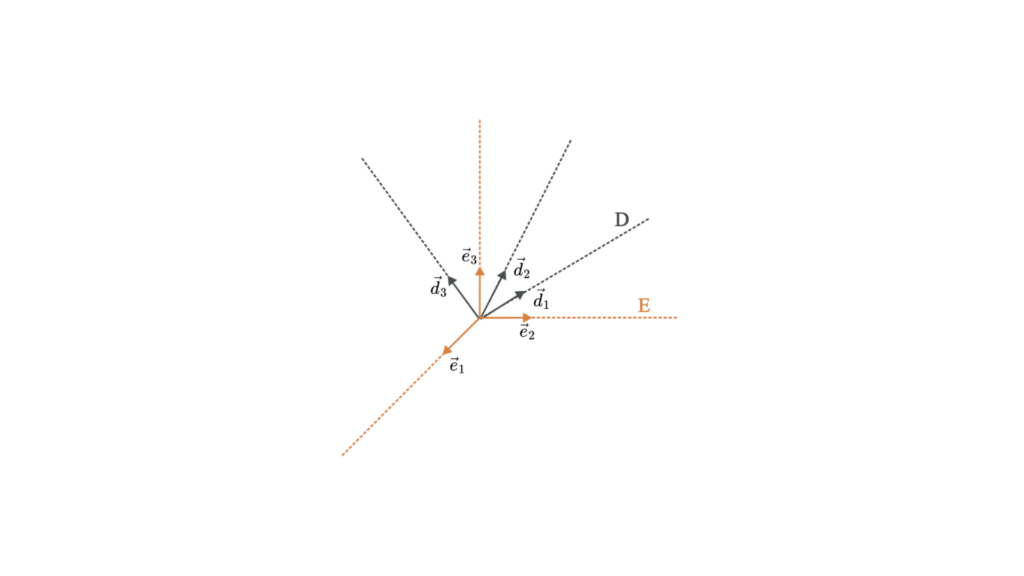
Rappresentazione matematica
Una matrice di coseni direttori 𝐶 è una matrice 3×3 che definisce la relazione tra due sistemi di coordinate:
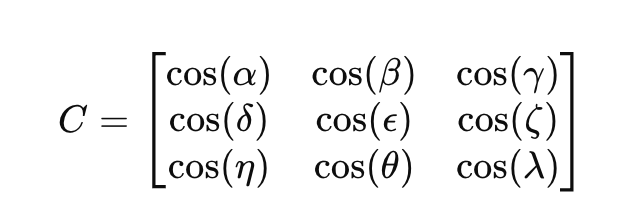
Dove gli elementi cos (⋅) rappresentano il coseno dell'angolo tra i vettori dei due sistemi di coordinate.
Ci parli del suo progetto