In der Navigation bezieht sich lage auf die Ausrichtung eines Fahrzeugs oder Objekts relativ zu einem festen Bezugsrahmen, der in der Regel durch drei Rotationsachsen definiert ist: nicken, rollen und gieren.
Diese Achsen beschreiben die Winkelposition und Bewegung des Fahrzeugs im dreidimensionalen Raum. nicken bezieht sich auf die Neigung der Fahrzeugnase nach oben oder unten, rollen steht für die seitliche Neigung des Fahrzeugs entlang seiner Längsachse und gieren bezeichnet die Drehung nach links oder rechts um seine vertikale Achse. Zusammen bestimmen diese Parameter, wie ein Fahrzeug in seiner Umgebung positioniert und manövriert wird.
lage ist entscheidend für die Aufrechterhaltung der Stabilität, die Gewährleistung einer präzisen Steuerung und die Ermöglichung einer genauen Navigation in verschiedenen Bereichen. In der Luftfahrt zum Beispiel hilft die lage Piloten oder Autopilotsystemen, die Flughöhe beizubehalten, Kurven auszuführen und Turbulenzen auszugleichen.
Auch in der maritimen Navigation sorgt die lage dafür, dass ein Schiff trotz der Herausforderungen durch Wellen und Strömungen aufrecht und auf Kurs bleibt.
In Raumfahrzeugen spielt die lage eine entscheidende Rolle bei der Ausrichtung von Antennen, Sonnenkollektoren oder wissenschaftlichen Instrumenten in die richtige Richtung, vor allem wenn externe visuelle Hinweise nicht verfügbar sind.
Zur Messung und Steuerung der lage werden Systeme wie Gyroskope, Beschleunigungsmesser und Magnetometer eingesetzt, die häufig in ein Trägheitsnavigationssystem (INS) integriert sind. Diese Systeme arbeiten mit externen Datenquellen wie GNSS oder Star-Trackern zusammen, um eine genaue Orientierung zu gewährleisten.
Das Verständnis und die Steuerung der lage sind besonders in dynamischen Umgebungen wichtig, in denen externe Kräfte wie Wind, Wellen oder Gravitationsanomalien die Flugbahn eines Fahrzeugs beeinflussen können.
Eine wirksame lage gewährleistet daher eine sichere und effiziente Fahrt und ermöglicht es den Fahrzeugen, ihre Navigationsziele mit Präzision zu erreichen.
lage
lage liefern die rollen, nicken und Gierwinkel, die die Ausrichtung eines Objekts im Raum beschreiben. Diese drei Komponenten sind für das Verständnis der lage des Objekts relativ zur Erdoberfläche oder zu einem Bezugsrahmen von wesentlicher Bedeutung.
- rollen bezieht sich auf die Drehung um die Vorwärtsachse, die sich auf die linke und rechte Neigung des Objekts auswirkt.
- nicken ist die Drehung um die seitliche Achse, die die Neigung nach oben und unten bestimmt.
- Gieren ist die Drehung um die vertikale Achse, die die Richtung angibt, in die das Objekt blickt.
Diese Lösungen kombinieren Daten von GNSS-Empfängern mit zusätzlichen Sensoren wie Beschleunigungsmessern und Gyroskopen, um hochpräzise und zuverlässige lage zu liefern.
Dieser Ansatz ist besonders wertvoll in Umgebungen, in denen eine präzise Orientierung entscheidend ist, wie bei Navigationssystemen für Flugzeuge, Schiffe und autonome Fahrzeuge. Durch die Integration dieser verschiedenen Sensoreingänge gewährleistet das System auch unter schwierigen Bedingungen eine optimale Leistung.
lage Vertretungen
lage steht für die Ausrichtung oder Drehung eines Objekts relativ zu einem Bezugsrahmen, z. B. der Erdoberfläche. In Navigationssystemen ist dieses Konzept von entscheidender Bedeutung für die Bestimmung der Ausrichtung des Objekts im Raum, was für Flugzeuge, UAVs, Schiffe oder andere autonome Systeme gelten könnte. Es gibt verschiedene Möglichkeiten, die lage mathematisch und visuell darzustellen.
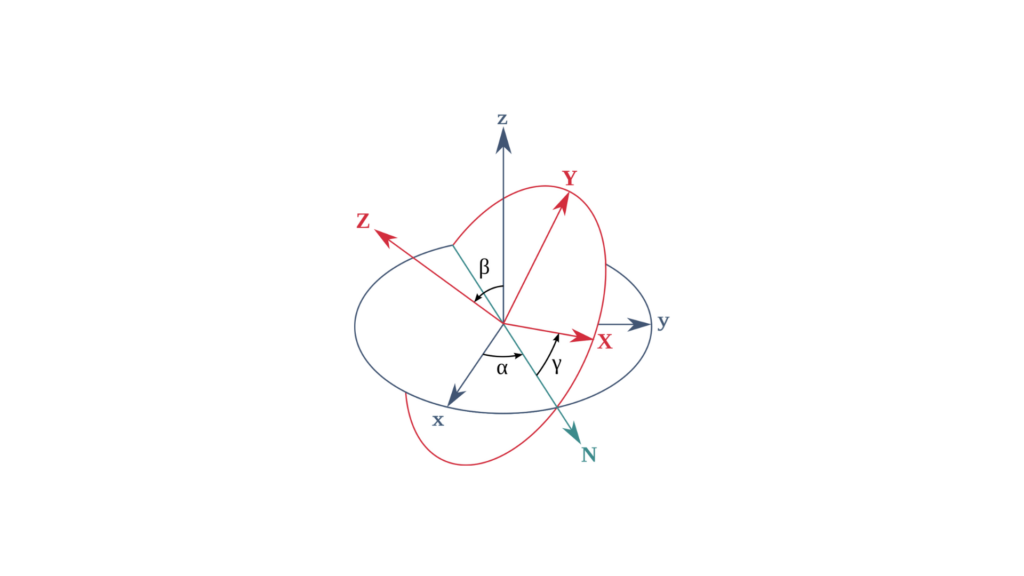
1 - Eulersche Winkelrollen, nicken, gieren)
Euler-Winkel stellen die Ausrichtung eines Objekts durch drei Drehungen dar: rollen, nicken und gieren. Diese Winkel beschreiben Drehungen um drei Achsen in einer bestimmten Reihenfolge, wie z. B.:
rollen (φ): Drehung um die Vorder- und Rückachse.
nicken(θ): Drehung um die Seite-zu-Seite-Achse.
Gieren(ψ): Drehung um die vertikale Achse.
Mathematische Darstellung
Euler-Winkel können als 3×3-Drehungsmatrix dargestellt werden, wobei:
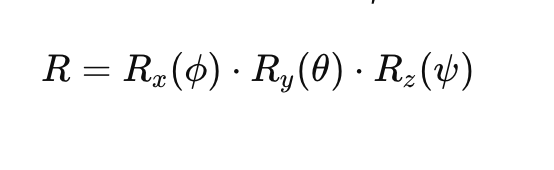
Hier:
- Rx(ϕ)R_x(\phi)Rx(ϕ) ist die Rotationsmatrix für rollen.
- Ry(θ)R_y(\theta)Ry(θ) ist die Rotationsmatrix für nicken.
- Rz(ψ)R_z(\psi)Rz(ψ) ist die Rotationsmatrix für Gieren.
Jede Rotationsmatrix wird wie folgt angegeben:
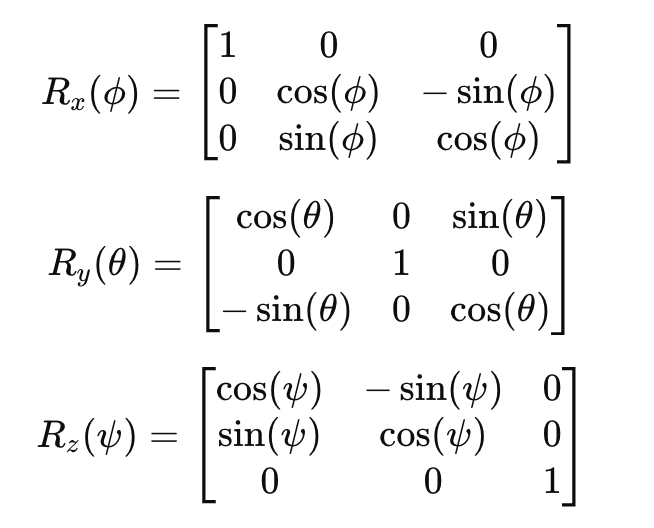
2 - Rotationsmatrizen
Rotationsmatrizen bieten eine alternative Möglichkeit zur Darstellung von lage. Bei dieser Methode beschreibt eine 3×3-Matrix die Ausrichtung eines Objekts im 3D-Raum relativ zu einem festen Koordinatensystem. Diese Matrizen sind orthogonal, d. h. die Zeilen und Spalten sind Einheitsvektoren. Folglich ist der Kehrwert der Matrix einfach ihre Transponierung.
Mathematische Darstellung
Eine allgemeine Rotationsmatrix 𝑅 lässt sich wie folgt beschreiben:
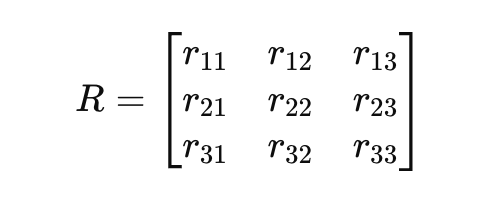
3 - Quaternionen
Quaternionen bieten eine kompaktere und numerisch stabilere Darstellung der Drehung. Sie vermeiden Singularitäten und Probleme mit der kardanischen Verriegelung, die mit Euler-Winkeln verbunden sind. Ein Quaternion 𝑞 ist ein 4-dimensionaler Vektor:
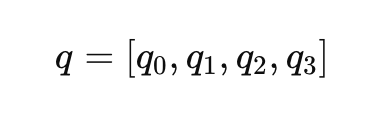
Dabei ist 𝑞0 der skalare Teil und [𝑞1, 𝑞2, 𝑞3] sind die Vektorkomponenten. Die Quaternionendarstellung einer Drehung kann wie folgt geschrieben werden:
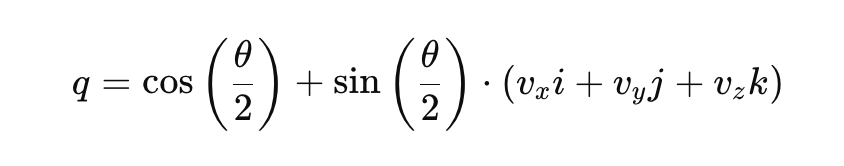
Hier:
- θ ist der Drehwinkel.
- [vx,vy,vz] ist der Einheitsvektor, der die Drehachse darstellt.
- i, j, k sind die grundlegenden Quaternioneneinheiten.
Vorteile von Quaternionen:
- Kardanische Blockierung und Singularitäten werden vermieden.
- Bei der Interpolation sind sie rechnerisch effizienter.
4 - Richtungskosinusmatrizen (DCM)
Eine Richtungskosinusmatrix ähnelt einer Drehmatrix und beschreibt ebenfalls die Ausrichtung eines Objekts. Die DCM setzt die Koordinaten eines Vektors in einem Koordinatensystem mit den Koordinaten desselben Vektors in einem anderen Koordinatensystem in Beziehung.
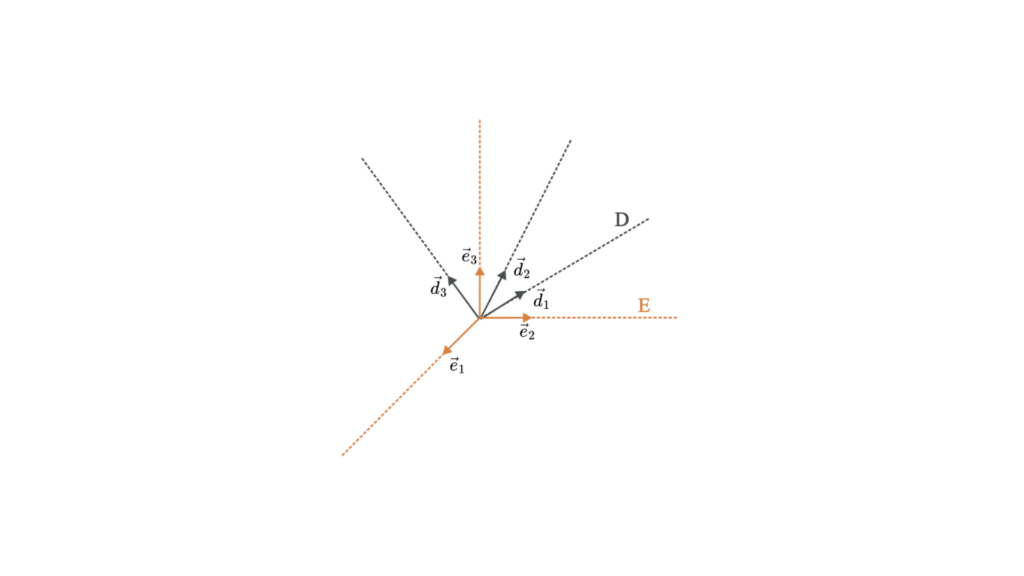
Mathematische Darstellung
Eine Richtungskosinusmatrix 𝐶 ist eine 3×3-Matrix, die die Beziehung zwischen zwei Koordinatenrahmen definiert:
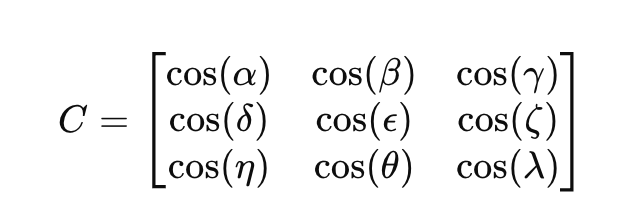
Dabei stellen die Elemente cos (⋅) den Kosinus des Winkels zwischen den Vektoren der beiden Koordinatensysteme dar.
Erzählen Sie uns von Ihrem Projekt