In this first article of our “Mastering Accuracy” series, we will explore Global Navigation Satellites Systems (GNSS) and their stand-alone accuracies taking into account the various errors.

 

What is a GNSS system?

 

Satellite-based positioning systems, like GPS, have become omnipresent, guiding us on our car journeys and our treks. They also play a critical role in various applications as diverse as autonomous vehicles, agriculture, and surveying.

However, it is important to move from the term “GPS” to the more inclusive “GNSS” (Global Navigation Satellite System), which encompasses all satellite constellations beyond just GPS.

There are four global satellite constellations in operation (GPS, GLONASS, GALILEO, BEIDOU). Additionally, there are supplementary constellations that serve local regions, like India’s IRNSS, or complement the global ones, such as Japan’s QZSS.

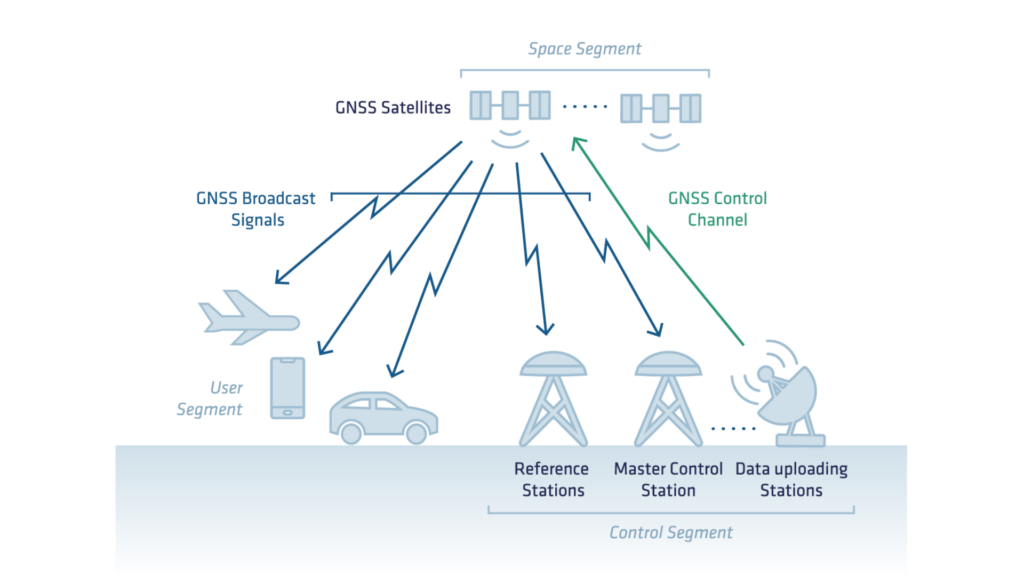
Apart from satellites, a GNSS system comprises of other essential segments:

• The satellite segment, which comprises the satellite constellation.
• The control segment, consisting of ground control stations and equipment. These are responsible for monitoring the constellations, determining the position of the satellites, and ensuring their continuous and correct operation.
• The user segment, which involves equipment used to calculate a position based on the signals received from the satellites.

 

GNSS fundamental principle: Trilateration

GNSS works by trilateration wherein signals from multiple satellites are used to determine receiver’s position and time. To determine a position, we need to solve four variables – latitude, longitude, altitude, and time.

Therefore, a minimum of four satellites is required; although more satellites enhance accuracy and reliability.

The following image shows how trilateration works. The distance between satellites can be seen as a sphere around the satellite.

The receiver’s position lies somewhere on these spheres. A second satellite can reduce the possible solutions to the intersection of these two spheres.

The third satellite makes it possible to find a single solution to the equation. In a real application, the time must also be evaluated, which requires a fourth satellite.

 

Signals emitted by the satellites

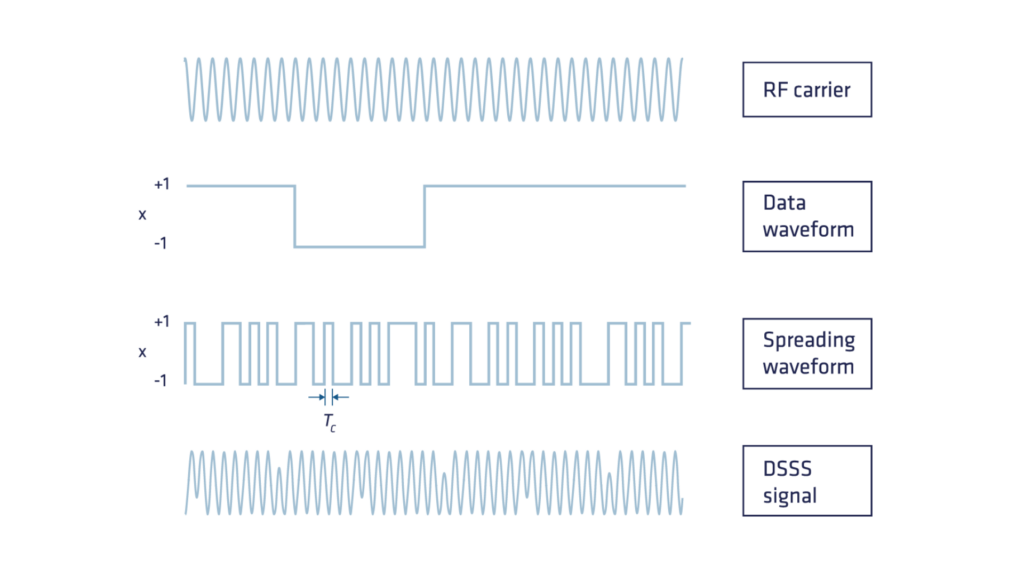
The GNSS satellites transmit signals across various frequency bands such as L1, L2, L5, among others. There are three basic components of GNSS signals:

• Navigation data (low frequency): computed by the control segment, this data includes essential information such as ephemeris data (Keplerian orbital parameters necessary for calculating satellite positions), clock correction data, and supplementary information. It is uploaded to the satellite and broadcasted globally to GNSS receivers.
• Pseudorandom noise code or PRN code (high frequency): a deterministic sequence of 0s and 1s designed with a predictable pattern to be able to be replicated by the receiver. Each satellite has a unique PRN code. The key advantage of adding the PRN code is that it allows multiple satellites to transmit signals in the same frequency simultaneously and be recognizable by the receiver. This technique is called CDMA (Code Division Multiple Access), with each satellite owning its unique pseudo random code. Only Glonass uses FDMA (Frequency Division Multiple Access) where each satellite has a slightly different frequency.
• RF carrier wave: a sinusoidal signal originally designed to transport the combined signal of navigation data and the PRN code. We will see later how this component evolves to become the foundation of the GNSS signal, enabling centimeter-level positioning accuracy.

 

Measuring distance to the satellite: code and carrier phase

Originally, the GPS system was designed so that the receiver utilizes a PRN code replica and auto-correlation techniques to compute the satellite-to-receiver range with submeter accuracy.

However, the carrier wave, initially intended for PRN code transmission, proved to be a valuable asset.

Carrier phase measurement, though more precise, introduced ambiguity in determining the distance between the satellite and the receiver. Further exploration of both measurements is presented below.

 

Satellite-to-receiver range computation with PRN Code

The GNSS receiver uses a process called “Delay Lock Loop” to determine the time delay between the transmitted code and the received code. This time delay, which corresponds to the signal propagation time, is then converted into a distance by multiplying it by the speed of light.

However, due to unsynchronized receiver and satellite clocks, the resulting distance is called pseudorange. In addition to the clock synchronization error, the pseudorange is affected by several other errors related to the propagation environment (atmosphere, hardware, etc.), which will be discussed later in the article.

 

Satellite-to-receiver range improvement: Carrier phase measurement

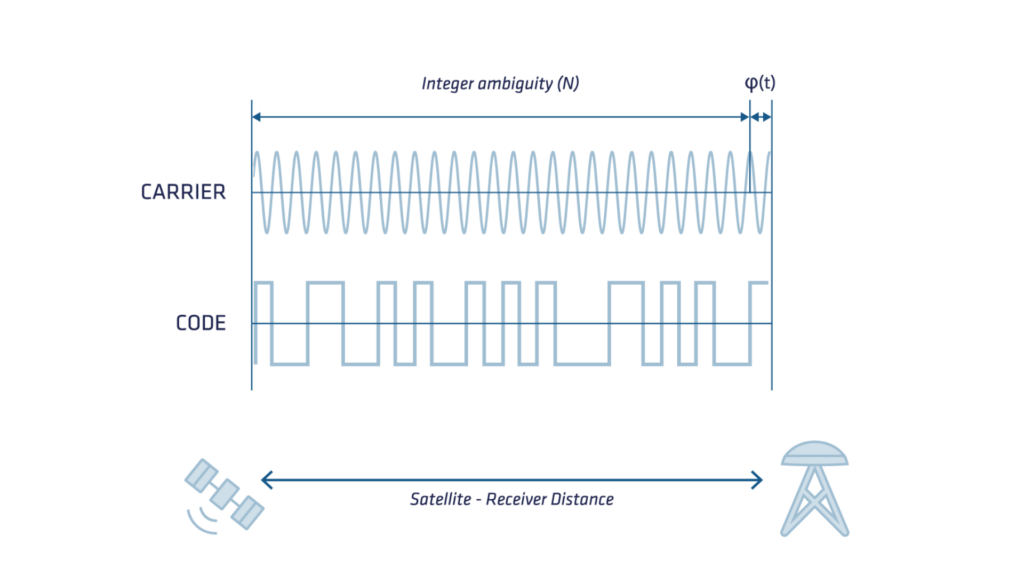
The distance between the satellite and the receiver can also be determined by counting the number of phase cycles elapsed between the signal emission and reception and multiplying this by the carrier wavelength.

This measurement is two orders of magnitude more precise than the code, but a constant unknown integer number of cycles (also known as ambiguity) affects its absolute accuracy.

To determine the precise evolution of the carrier phase, the GNSS receiver accumulates the Doppler frequency shifts in the carrier wave, caused by the satellite to receiver relative motion.

In case of signal disruption, this accumulation process cannot account for the actual motion and abrupt jumps in the measurement, also known as “cycle slips,” can be observed.

Correctly handing the cycle slips, and the ambiguity are challenging and key aspects of precise positioning techniques such as Real Time Kinematics (RTK) and Precise Point Positioning (PPP).

The following diagram shows the signal carrier wave, the code and their respective resolutions.

Sources of errors in GNSS

The initial general public accuracy (non-military) of GPS was around 100m. Following the multiple years of evolutions (removal of selective availability, deployment of new constellations and SBAS systems, new satellites, and new frequencies,) the accuracy of standalone GNSS is now between 5m for entry level GNSS receivers, down to 1m for high-end ones.

The accuracy of the GNSS positioning is influenced by the various source of errors that accumulate:

 

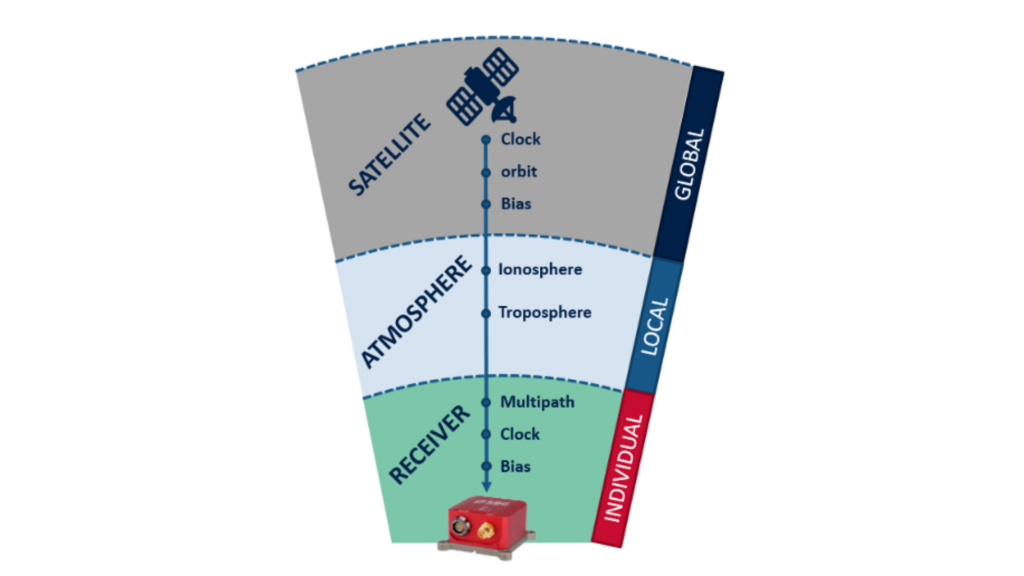
Satellite errors

• Clock errors: While the atomic clocks on GNSS satellites are highly precise, they experience minor drift. Unfortunately, even a slight deviation in the satellite clock can lead to a substantial discrepancy in the calculated position by the receiver. For instance, a mere 10 nanoseconds of clock error translate to a position error of 3 meters on the range measurement!
• Orbit errors: While GNSS satellites follow highly precise and well-documented orbits, these orbits undergo minor variations, similar to the satellite clocks. Like clock inaccuracies, even a slight change in the satellite orbit can cause a significant error in the calculated position. Residual errors in the orbit persist, contributing to potential position errors of up to ±2.5 meters.

 

Atmospheric Errors

• Ionospheric Delay: Situated between 50 to 1,000 km above the Earth, the ionosphere contains charged ions affecting radio signal transmission, causing position errors (typically ±5 meters, higher during heightened ionospheric activity). Ionospheric delay varies with solar activity, daytime, season, and location, making predictions challenging.
• Tropospheric Delay: The Earth’s immediate atmospheric layer, the troposphere, sees variations in delay due to shifts in humidity, temperature, and atmospheric pressure.

 

Receiver errors

• The receiver’s internal clock, which are less accurate when compared to the satellite’s atomic clock, along with other hardware and software errors add noise and bias to the measurements.

Delay	Origin	Magnitude
Position Error	Satellite	5 m
Clock Offset	Satellite	0-300 km
Instrumental Delay	Satellite	1-10 m
Relativistic Effect	Satellite	10 m
Ionospheric Delay	Path (50-1000 km)	2-50 m
Tropospheric Delay	Path (0-12 km)	2-10 m
Instrumental Delay	Receiver	1-10 m
Clock Offset	Receiver	0-300 km

 

These errors should be accounted for, mitigated using a specific error model or estimated by the navigation filter to ensure optimal navigation.

Many other error terms are not listed in this article, such as tidal effects or relativistic effects, and should also be considered for during position computation.