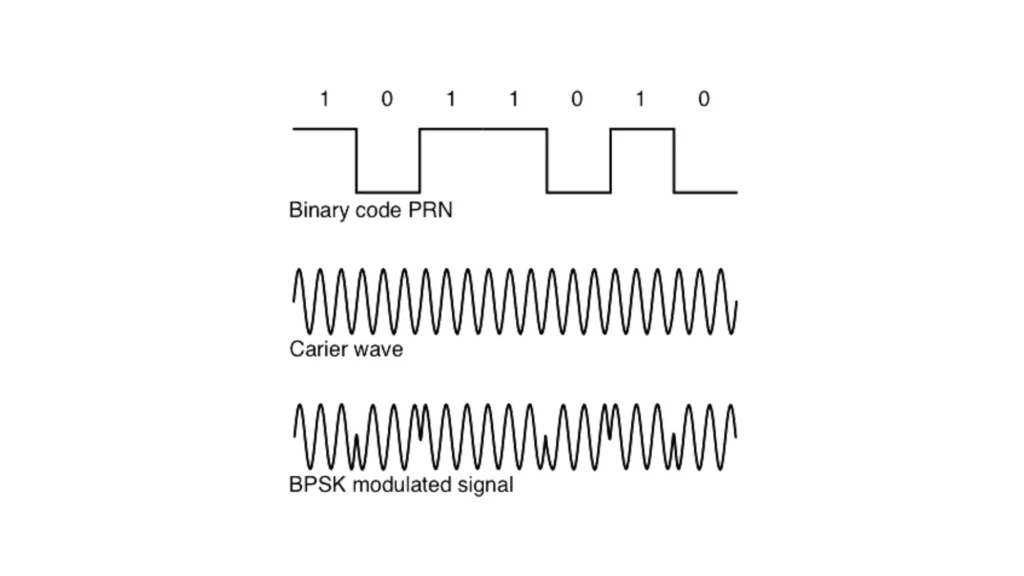
Un code de bruit pseudo-aléatoire (PRN) génère une séquence binaire qui semble aléatoire mais qui reste déterministe et reproductible. Les systèmes de navigation par satellite, tels que GPS, Galileo et BeiDou, ainsi que diverses applications de communication, reposent sur ces codes.
Les codes PRN offrent des caractéristiques clés qui les rendent essentiels à la navigation et à la communication.
Ils suivent un modèle déterministe puisque les algorithmes les génèrent, assurant une reproduction précise. Malgré leur conception structurée, ils présentent des propriétés statistiques similaires au bruit blanc, ce qui les fait apparaître aléatoires.
Les ingénieurs conçoivent différents codes pour qu'ils soient orthogonaux ou uniques, ce qui réduit la corrélation croisée et minimise les interférences.
Dans les applications GPS et GNSS (par exemple, les systèmes d'aéronefs sans pilote), chaque satellite de la constellation transmet un code PRN unique.
Ces codes remplissent de multiples fonctions : ils aident les récepteurs GPS à distinguer les signaux provenant de différents satellites, permettent le calcul de la portée en comparant les codes transmis avec une version générée localement pour déterminer le temps de trajet du signal et prennent en charge la modulation à spectre étalé.
Cette technique de modulation permet aux signaux de transmettre sur une large bande passante, augmentant ainsi la résistance aux interférences et au brouillage.
Le GPS utilise différents types de codes PRN. Le code C/A (Coarse/Acquisition) prend en charge la navigation GPS standard et se répète toutes les 1 milliseconde. Le code P(Y), conçu pour les applications militaires, crypte ses données et se répète tous les sept jours.
Le code M, une version militaire avancée, améliore les capacités anti-brouillage.
Les registres à décalage à rétroaction linéaire (LFSR) génèrent des codes PRN, produisant des séquences avec des propriétés de corrélation souhaitables pour un suivi précis du signal.
En conservant des caractéristiques pseudo-aléatoires tout en assurant la prévisibilité et la répétabilité, les LFSR rendent ces codes très fiables pour la navigation et la communication.
Représentation mathématique du code PRN
Pour G1 et G2, la relation de récurrence est la suivante :
G1(n) = G1(n−3) ⊕ G1(n−10)
G2(n) = G2(n−2) ⊕ G2(n−3) ⊕ G2(n−6) ⊕ G2(n−8) ⊕ G2(n−9) ⊕ G2(n−10)
Où ⊕ (XOR) est l'opération d'addition binaire.
Le code PRN est alors formé comme suit :
PRN(n) = G1(n) ⊕ G2 (n+delay)
Le délai varie pour chaque satellite GPS, ce qui garantit des séquences PRN uniques.