The Extended Kalman Filter (EKF) is a powerful tool used in navigation and control systems for estimating the state of a system that evolves over time. It is an extension of the Kalman Filter, designed to handle non-linear systems, making it crucial for applications where the relationship between variables is not linear.
This powerful algorithm is used to estimate the state of a dynamic system based on noisy sensor measurements. It builds on the standard Kalman Filter by accommodating non-linear systems, which are common in real-world navigation scenarios. While the traditional Kalman Filter assumes linear dynamics and Gaussian noise, the EKF overcomes these limitations by linearizing the non-linear system around the current estimate. This allows it to operate effectively in more complex, real-life environments.
Basic principle of Extended Kalman filter
At its core, the EKF continuously updates a state vector—a set of variables that describe the system’s current condition, such as position, velocity, and orientation in navigation contexts. It relies on a process model to predict how the state evolves over time, incorporating system dynamics and control inputs. Meanwhile, the measurement model links incoming sensor data to the estimated state, and a covariance matrix represents the uncertainty in both predictions and observations, helping the EKF balance confidence between model estimates and sensor inputs.
The filter operates in two main phases: prediction and update. During the prediction phase, it uses the process model to forecast the next state and predict the associated uncertainty by updating the covariance matrix. To manage non-linearity, the EKF linearizes both the process and measurement models using Jacobian matrices—mathematical representations that approximate how the system behaves near the current estimate.
In the update phase, the EKF incorporates new sensor measurements to refine its prediction. It calculates the Kalman Gain, which determines how much weight to assign to the new measurements versus the predicted state. This gain enables the EKF to adjust the state estimate accordingly and update the covariance to reflect the reduced uncertainty after the measurement.
Applying the EKF in modern applications
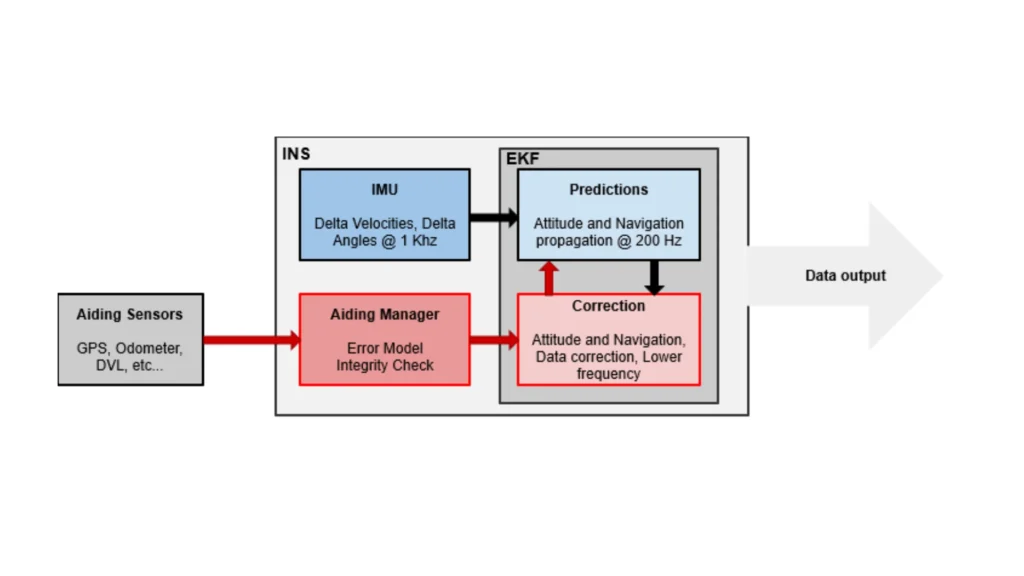
The EKF is widely used in modern navigation systems due to its ability to deliver accurate state estimates in the presence of noise and system complexity. For instance, Inertial Navigation Systems (INS) rely on accelerometers and gyroscopes, which are prone to drift and noise. The EKF combines sensor data to provide stable estimates of position, velocity, and orientation for dynamic platforms. These estimates are critical for the reliable operation of autonomous vehicles, aircraft, and other mobile systems.
In robotics and autonomous systems, the EKF enables robust localization and mapping. Robots use sensors like LiDAR or cameras to estimate position and update maps using an Extended Kalman Filter (EKF). This enables real-time mapping and localization, supporting safe and autonomous operation in unfamiliar or dynamic environments.
In aerospace and defense, the EKF plays a vital role in guidance and tracking systems. It enables aircraft, missiles, and spacecraft to maintain precise position and trajectory, even under non-linear motion conditions. The EKF continues to operate reliably when exposed to external disturbances that could otherwise degrade navigation accuracy.
The technology behind the EKF includes several critical components. Jacobian matrices support the linearization process, while sensor fusion integrates data from multiple sources to ensure resilience and accuracy. To support real-time operation, the EKF depends on efficient computational algorithms for matrix operations, covariance updates, and measurement integration.
In conclusion, the Extended Kalman filter (EKF) is an essential tool in advanced navigation systems. By extending the Kalman Filter to handle non-linear systems, you get accurate and real-time state estimation. It supports a wide range of applications, including robotics, automotive ADAS, aerospace, and defense systems. Mastering the EKF’s principles and technologies is key to developing high-performance navigation solutions in complex and dynamic environments.