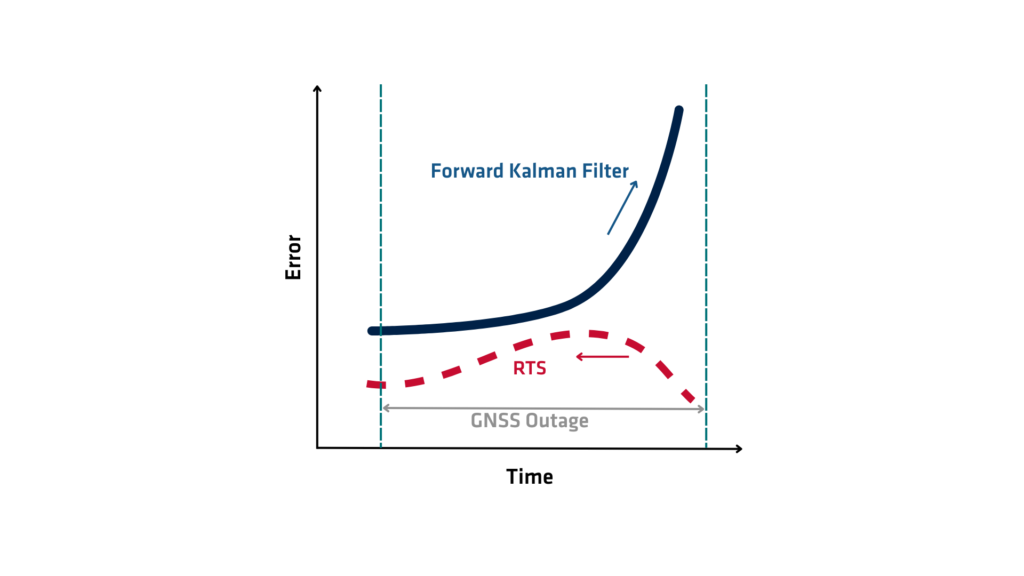
The RTS (Rauch-Tung-Striebel) smoother is a mathematical algorithm used to improve the accuracy of state estimation in dynamic systems. It belongs to the family of smoothing algorithms and extends the capabilities of the Kalman filter, which estimates the state of a system in real time. While the Kalman filter processes data sequentially and estimates the current state based solely on past and present measurements, the RTS smoother goes a step further by using both past and future measurements to refine state estimates retrospectively. This process results in significantly more accurate state estimations, especially in applications that involve post-processing of data.
How does RTS works ?
The RTS (Rauch-Tung-Striebel) or RTS smoother operates in two main stages: the forward pass and the backward pass. During the forward pass, the algorithm runs a standard Kalman filter through the data, collecting estimates of the state and associated error covariances at each time step. This stage essentially lays the groundwork by providing the initial state estimates and uncertainty measures, based only on past data up to each point in time.
Once the forward pass is complete, the backward pass begins. The algorithm works its way backward from the final state estimate toward the initial one. At each time step, the RTS (Rauch-Tung-Striebel) revises the state estimate by incorporating information from future time steps—information that was not available during the forward filtering process. It uses the Kalman gain, transition matrices, and covariances calculated in the forward pass to compute a smoothed estimate that balances both past and future observations. This backward recursion corrects the filtered estimates, reducing the overall estimation error and producing a more consistent and accurate trajectory of the system states
Mathematically, the smoother applies a correction step that leverages the correlation between errors in successive estimates. By modeling the system’s evolution through a linear Gaussian process, the RTS smoother assumes the same dynamics and measurement models used in the Kalman filter. It calculates a smoothing gain at each step, which determines how much of the future estimate should be used to adjust the current estimate. This gain depends on the covariance matrices of the filtered estimates and the predicted state.
Advantages of RTS (Rauch-Tung-Striebel)
The RTS smoother produces a globally optimal estimate for the entire sequence of system states. It assumes the models are linear and Gaussian. Filtering estimates only the current state. Smoothing reconstructs the best past state estimates using all available data. This makes smoothing especially valuable for offline applications.
The RTS smoother finds application in various domains, including aerospace navigation, signal processing, finance, and robotics. In inertial navigation systems (INS), for example, it is often used to post-process trajectory data to reduce drift and noise. Similarly, time-series analysis or object tracking uses it to refine real-time estimates and recover accurate paths or trends.
The RTS smoother offers advantages but needs full dataset access and becomes computationally intensive for long or complex data. It also relies heavily on the assumption of linear dynamics and Gaussian noise. Use the Extended or Unscented RTS smoother when the system is non-linear or the noise is non-Gaussian. These variants adapt the method to non-linear filters like the Extended Kalman Filter (EKF) or Unscented Kalman Filter (UKF).
The RTS smoother refines Kalman filtering by using future data to update past estimates, improving accuracy and stability. It forms the foundation of state estimation and enables precise reconstruction of dynamic systems using post-processed data.