A gyroscope is a sensor that measures the rotation rate with respect to an inertial frame. Consequently, it captures all subsequent changes in orientation when rotated. Moreover, since the Earth coordinate frame itself is rotating, a gyroscope lying on the ground will also detect the Earth’s rotation rate—approximately 15° per hour. Gyroscopes typically express output in degrees per second (°/s) or radians per second (rad/s).
How does it work?
In practical applications, systems integrate rotation rates at high frequency to determine sensor orientation with great precision. Therefore, this principle forms the foundation of all inertial sensors, including Vertical Gyroscopes, Attitude and Heading Reference Systems (AHRS), Motion Reference Units (MRU), and Inertial Navigation Systems (INS).
Furthermore, these play a critical role in determining position and velocity within INS frameworks. In addition, the highest-performance gyroscopes—usually closed-loop fiber optic gyroscopes (FOG)—directly measure Earth’s rotation without needing bias estimation. As a result, these sensors can determine heading without relying on any external reference, a functionality known as gyrocompassing. However, alternative techniques also exist to determine heading, which helps reduce strict constraints on this technology.
The Coriolis and Sagnac effects in gyroscopes
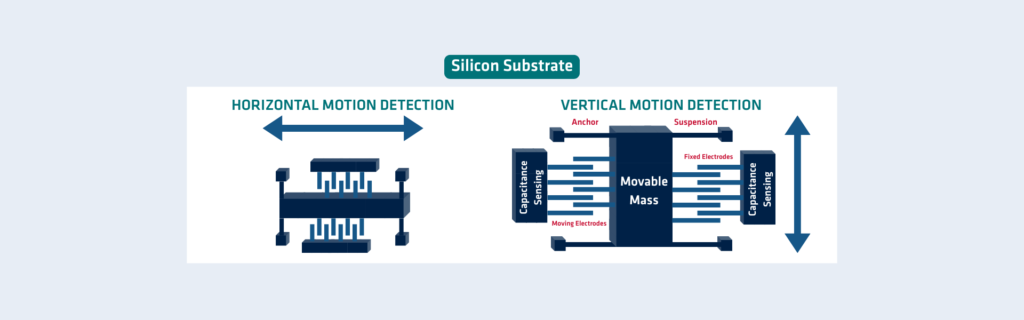
Regarding their operating principle, SBG Systems gyroscopes utilize two core physical effects to measure rotation: the Coriolis effect and the Sagnac effect. Specifically, the Coriolis effect is used by MEMS gyroscopes. When a proof mass vibrates in the X direction, a rotation around the perpendicular Z axis generates a force that causes motion along the Y axis.
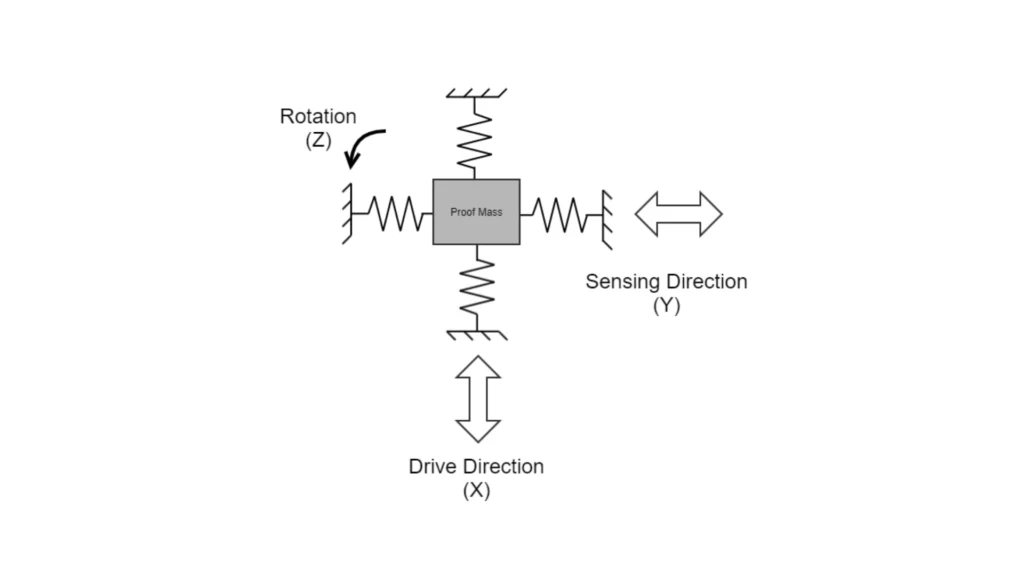
Accordingly, several MEMS architectures implement this principle, typically using vibrating beams or rings. Notably, the actual performance of these gyroscopes varies depending on factors like MEMS element size and quality, sensor packaging, and mechanical and signal processing techniques.
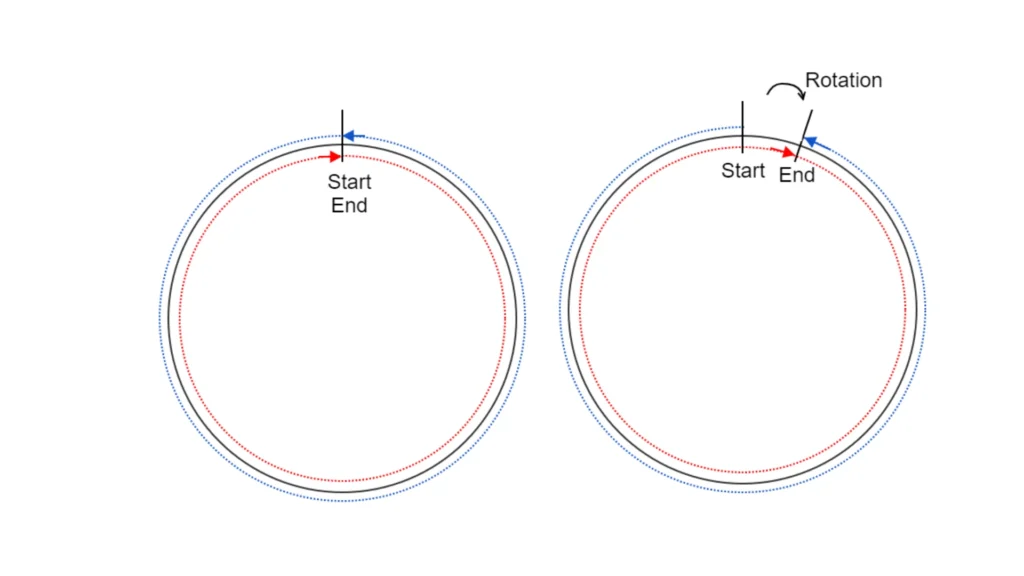
Optical gyroscopes, such as FOGs, employ the Sagnac effect to measure rotation. In this method, two light sources loop in opposite directions—one clockwise and the other counterclockwise. When there is no rotation, the light waves arrive simultaneously; however, during rotation, one path lengthens while the other shortens. Consequently, this generates interference, which can be measured to deduce angular speed.
Applications of gyroscopes in inertial navigation
Together, these principles enable gyroscopes to deliver precise and reliable motion data across a wide range of applications.
Aviation
In aviation, these are critical for aircraft navigation and stability. They are used in the following systems:
- Attitude Indicators: These instruments display the aircraft’s orientation relative to the horizon, helping pilots maintain proper pitch and roll angles.
- Autopilot Systems: Gyroscopes provide feedback to autopilot systems, allowing for automatic control of the aircraft’s heading, altitude, and course.
- Inertial Navigation Systems (INS): INS rely on gyroscopes to track the aircraft’s movement and orientation, providing accurate positioning information even when GPS signals are unavailable.
Maritime navigation
Concerning maritime navigation, gyroscopes assist in maintaining the stability and course of ships and submarines:
- Gyrocompasses: Gyrocompasses provide accurate directional information, independent of the Earth’s magnetic field, helping navigators maintain a steady course.
- Stabilization systems use these sensors to reduce rolling and pitching, enhancing passenger comfort and ensuring safety.
Space
For spacecraft and satellites, gyroscopes are essential for orientation and control:
- Attitude Control Systems: Gyroscopes help control the orientation of spacecraft by providing precise measurements of rotational movements, crucial for tasks such as docking, positioning, and maneuvering.
- Inertial Measurement Units (IMUs): IMUs, which include gyroscopes, provide navigation and stabilization to ensure accurate positioning and control in space.